Гипотеза плоских сечений при изгибе
Гипотезу плоских сечений при изгибе можно объяснить на примере: нанесем на боковой поверхности недеформированной балки сетку, состоящую из продольных и поперечных (перпендикулярных к оси) прямых линий. В результате изгиба балки продольные линии примут криволинейное очертание, а поперечные практически останутся прямыми и перпендикулярными к изогнутой оси балки.
Формулировка гипотезы плоских сечения: поперечные сечения, плоские и перпендикулярные к оси балки до деформации, остаются плоскими и перпендикулярными к изогнутой оси после ее деформации.
Это обстоятельство свидетельствует: при изгибе выполняется гипотеза плоских сечений, как при растяжении и кручении
Помимо гипотезы плоских сечений принимается допущение: продольные волокна балки при ее изгибе не надавливают друг на друга.
Гипотезу плоских сечений и допущение называют гипотезой Бернулли.
Рассмотрим балку прямоугольного поперечного сечения, испытывающую чистый изгиб (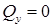 ). Выделим элемент балки длиной
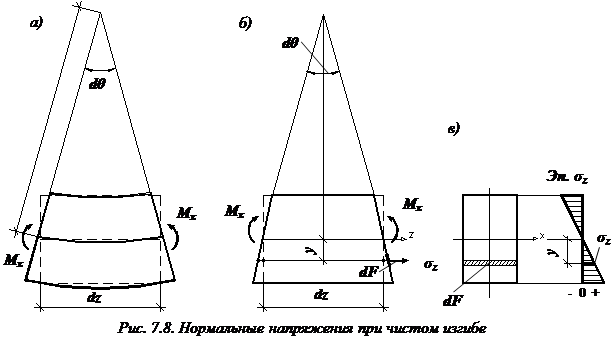
). Выделим элемент балки длиной 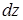 (рис. 7.8. а). В результате изгиба поперечные сечения балки повернутся, образовав угол
(рис. 7.8. а). В результате изгиба поперечные сечения балки повернутся, образовав угол 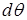 . Верхние волокна испытывают сжатие, а нижние растяжение. Радиус кривизны нейтрального волокна обозначим
. Верхние волокна испытывают сжатие, а нижние растяжение. Радиус кривизны нейтрального волокна обозначим 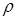 .
.
Условно считаем, что волокна изменяют свою длину, оставаясь при этом прямыми (рис. 7.8. б). Тогда абсолютное и относительное удлинения волокна, отстоящего на расстоянии y от нейтрального волокна:
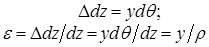
По закону Гука:
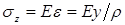
Покажем, что продольные волокна, не испытывающие при изгибе балки ни растяжения, ни сжатия, проходят через главную центральную ось x.
Поскольку длина балки при изгибе не изменяется, продольное усилие (N), возникающее в поперечном сечении, должно равняться нулю. Элементарное продольное усилие 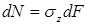 .
.
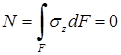
С учетом выражения 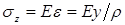 :
:
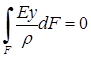
 Множитель
Множитель 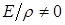 можно вынести за знак интеграла (не зависит от переменной интегрирования).
можно вынести за знак интеграла (не зависит от переменной интегрирования).
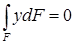
Выражение представляет статический момент инерции поперечного сечения балки относительно нейтральной оси x. Он равен нулю, когда нейтральная ось проходит через центр тяжести поперечного сечения. Следовательно, нейтральная ось (нулевая линия) при изгибе балки проходит через центр тяжести поперечного сечения.
Очевидно: изгибающий момент связан с нормальными напряжениями, возникающими в точках поперечного сечения стержня. Элементарный изгибающий момент, создаваемый элементарной силой 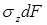 :
:
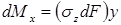 ,
,
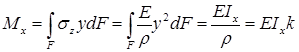
где 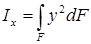 – осевой момент инерции поперечного сечения относительно нейтральной оси x, а отношение
– осевой момент инерции поперечного сечения относительно нейтральной оси x, а отношение 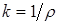 - кривизна оси балки.
- кривизна оси балки.
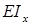 - жесткость балки при изгибе (чем больше, тем меньше радиус кривизны
- жесткость балки при изгибе (чем больше, тем меньше радиус кривизны 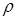 ).
).
Полученная формула 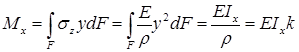 представляет собой закон Гука при изгибе для стержня: изгибающий момент, возникающий в поперечном сечении, пропорционален кривизне оси балки.
представляет собой закон Гука при изгибе для стержня: изгибающий момент, возникающий в поперечном сечении, пропорционален кривизне оси балки.
Выражая из формулы закона Гука для стержня при изгибе радиус кривизны (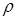 ) и подставляя его значение в формулу
) и подставляя его значение в формулу 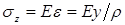 , получим формулу для нормальных напряжений (
, получим формулу для нормальных напряжений (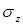 ) в произвольной точке поперечного сечения балки, отстоящей на расстоянии y от нейтральной оси x:
) в произвольной точке поперечного сечения балки, отстоящей на расстоянии y от нейтральной оси x: 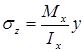 .
.
В формулу для нормальных напряжений (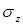 ) в произвольной точке поперечного сечения балки следует подставлять абсолютные значения изгибающего момента (
) в произвольной точке поперечного сечения балки следует подставлять абсолютные значения изгибающего момента (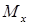 ) и расстояния от точки до нейтральной оси (координаты y). Будет ли напряжение в данной точке растягивающим или сжимающим легко установить по характеру деформации балки или по эпюре изгибающих моментов, ординаты которой откладываются со стороны сжатых волокон балки.
) и расстояния от точки до нейтральной оси (координаты y). Будет ли напряжение в данной точке растягивающим или сжимающим легко установить по характеру деформации балки или по эпюре изгибающих моментов, ординаты которой откладываются со стороны сжатых волокон балки.
Из формулы 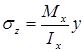 видно: нормальные напряжения (
видно: нормальные напряжения (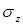 ) изменяются по высоте поперечного сечения балки по линейному закону. На рис. 7.8, в показана эпюра нормальных напряжений. Наибольшие напряжения при изгибе балки возникают в точках, наиболее удаленных от нейтральной оси. Если в поперечном сечении балки провести линию, параллельную нейтральной оси x, то во всех ее точках возникают одинаковые нормальные напряжения.
) изменяются по высоте поперечного сечения балки по линейному закону. На рис. 7.8, в показана эпюра нормальных напряжений. Наибольшие напряжения при изгибе балки возникают в точках, наиболее удаленных от нейтральной оси. Если в поперечном сечении балки провести линию, параллельную нейтральной оси x, то во всех ее точках возникают одинаковые нормальные напряжения.
Несложный анализ эпюры нормальных напряжений показывает, при изгибе балки материал, расположенный вблизи нейтральной оси, практически не работает. Поэтому в целях снижения веса балки рекомендуется выбирать такие формы поперечного сечения, у которых большая часть материала удалена от нейтральной оси, как, например, у двутаврового профиля.