Осевой, полярный и центробежный моменты инерции фигуры
Осевой момент инерции фигуры - это интеграл произведений элементарных площадей на квадраты их расстояний до рассматриваемой оси. Формулы осевого момента инерции произвольной фигуры (см. рис. 4.1) относительно осей x и y:

Полярный момент инерции фигуры относительно данной точки (полюса) - это интеграл произведений элементарных площадей на квадраты их расстояний до полюса:
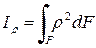
Если через полюс проведена система взаимно перпендикулярных осей x и y, то  , и формула полярного момента инерции равна сумме осевых моментов инерции относительно осей x и y:
, и формула полярного момента инерции равна сумме осевых моментов инерции относительно осей x и y:
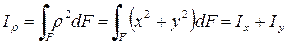
Из формул осевых  и полярного
и полярного 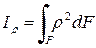 моментов инерции видно: значения осевых и полярного моментов инерции всегда положительны, так как координаты
моментов инерции видно: значения осевых и полярного моментов инерции всегда положительны, так как координаты 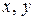 и расстояние
и расстояние 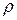 возведены в квадрат.
возведены в квадрат.
Центробежный момент инерции фигуры - это интеграл произведений элементарных площадей на их расстояния до осей x и y:
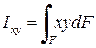
Моменты инерции измеряются в единицах длины в четвертой степени (как правило, см4).
Понятие момента инерции поперечного сечения ввел в 1834 г. французский ученый Н. Перси.